A non parametric approach for histogram segmentation
Fine to Coarse Segmentation Algorithm
The following algorithm segments a 1D-histogram without a priori assumptions about the underlying density
function, as described in
[1] J. Delon, A. Desolneux, J-L. Lisani et A-B. Petro, A non parametric approach
for histogram segmentation, IEEE Transactions on Image
Processing, vol.16, no 1, pp.253-261, Janvier 2007 (pdf).
Let h be a discrete histogram, with N samples on L bins {1,...,L}.
h(i) denotes the value of h in the bin i.
For each interval [a,b], h(a,b)=h(a)+ h(a+1)+... +h(b).
- Let S={s(0),...,s(n)} be the list of all the local minima, plus the endpoints 1 and L of the histogram h. n is termed "length" of the segmentation.
- Choose i randomly in [1; length(S)-1].
- For each t in the interval [s(i-1); s(i+1)], compute the increasing Grenander estimator hc of h on the interval [s(i-1),t] and the decreasing Grenander estimator hd of h on the interval [t,s(i+1)] thanks to the Pooling Adjacent Violators algorithm described below.
Let Lc= t- s(i-1)+1 be the length of the interval [s(i-1),t] and Nc= h(s(i-1),t) its number of samples (respectively Ld=s(i+1)-t+1 and Nd= h(t,s(i+1) the length and number of samples of [t,s(i+1)]).
- For each sub-interval [a,b] of [s(i-1); t], compute
where B(N,k,p) denotes the binomial tail
If NFAc[a,b] <= 1/2, then [a,b] is said to be a meaningful rejection for the increasing hypothesis on [s(i-1); t] (see [1] for the interpretation of the bound 1/2);
- In the same way, for each sub-interval [a,b] of [t; s(i+1)], compute NFAd[a,b]. If NFAd[a,b] <= 1/2 then [a,b] is a meaningful rejection for the decreasing hypothesis on [t; s(i+1)].
- If there exists t in [s(i-1); s(i+1)] with no rejection of the increasing hypothesis on [s(i-1),t] and no rejection of the decreasing hypothesis on [t,s(i+1)], then [s(i-1); s(i+1)] is said to follow the unimodal hypothesis.
In this case, merge the intervals [s(i-1); s(i)] and [s(i); s(i+1)] and remove s(i) from S.
- Repeat step 2 until no more pair of successive intervals follows the unimodal hypothesis.
-
Repeat steps 2 and 3 with the unions of j segments, j going from 3 to length(S).
Hint
When N is too large, the computation of the binomial tail can be replaced by a large deviation approximation
The Pooling Adjacent Violators algorithm
The following algorithm [2, 3] computes the decreasing Grenander estimator of a histogram r (apply it to -r to compute the increasing estimator). In order to compute the Grenander decreasing estimator of a histogram h on a given interval I, replace r in the following by the histogram h restricted to I.
Repeat the following operation until you get a decreasing distribution:
- For each interval [i,j] on which
r is increasing, i.e. r(i) <= r(i+1) <= ... <= r(j) and r(i-1) >= r(i) and
r(j+1) < r(j), replace the values {r(i),... r(j)} in r by the mean value on the interval: (r(i)+...+ r(j))/(j-i+1).
[2] AYER, M., BRUNK, H., EWING, G., REID, W., AND SILVERMAN,
E. An empirical distribution function for sampling with incomplete
information. The Annals of Mathematical Statistics 26, 4 (1955), 641--
647.
[3] BIRGÉ, L. The Grenander estimator: A nonasymptotic approach. The
Annals of Statistics 17, 4 (1989), 1532--1549.
![\begin{displaymath}NFA_c([a,b])=
\begin{cases}
\frac{L_c(L_c+1)}{2} \mathcal{B}(...
...b)}{N_c}) &\;\;\;
\text{ if }\;\;
h(a,b) < hc(a,b).
\end{cases}\end{displaymath}](img1.png)
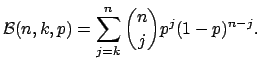
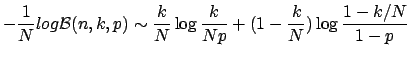 if
if 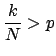 with
with